Information Leakage via Non-Uniform Coefficient Generation

[ThewsyRum]

Summary

I discovered a cryptographic vulnerability in the implementation of the Shamir Secret Sharing scheme. The implementation explicitly forbids polynomial coefficients from colliding with the secret byte or with each other. This rejection sampling introduces a statistical bias that violates the Information-Theoretic Security property of Shamir's scheme. It allows an attacker with $t-1$ shares to rule out specific candidates for the secret byte, thereby reducing the effective entropy of the key.

Introduction

In a standard Shamir Secret Sharing Scheme over $GF(256)$, a secret $S$ is protected by a polynomial $f(x) = S + a_1x + a_2x^2 + \dots + a_{t-1}x^{t-1}$.
For the scheme to maintain perfect secrecy, the coefficients $a_1, \dots, a_{t-1}$ must be chosen uniformly and independently at random from the field $GF(256)$. The probability of any coefficient $a_i$ taking a specific value $v$ must be $1/256$, regardless of the value of $S$.

The current implementation forces coefficients to be distinct from the secret and distinct from each other.

Code snippet:

        for (let b = 0; b < secret.length; b++) {
            let q = [secret[b]];

            for (let i = 0; i < threshold - 1; i++) {
                do {
                    // ... entropy generation ...
                    w  = e[ePointer++];
                } while (q.includes(w)); // <--- VULNERABILITY
                q.push(w);
            }
            // ...

By using while (q.includes(w)), the code enforces that $a_i \neq S$ and $a_i \neq a_j$ (for $i \neq j$). This constraint does not exist in the Python(pybtc) implementation, creating a cross-library inconsistency and a security flaw in the JS version.

Attack (Entropy Reduction)

An attacker possessing $t-1$ shares can perform the following attack on each byte of the secret:

1. Iterate through all 256 possible candidates for the Secret Byte ($S_{guess}$).
2. Using Lagrange interpolation (or system of linear equations), derive the implied coefficients $a_1, \dots, a_{t-1}$ that would result in the held shares if $S_{guess}$ were the true secret.
3. Check the constraint: If any derived $a_i == S_{guess}$ or $a_i == a_j$, then $S_{guess}$ is impossible under this specific implementation.
4. Eliminate $S_{guess}$ from the search space.

In a correct implementation, every $S_{guess}$ would produce a valid polynomial. In this faulty implementation, valid secrets are rejected, leaking information.

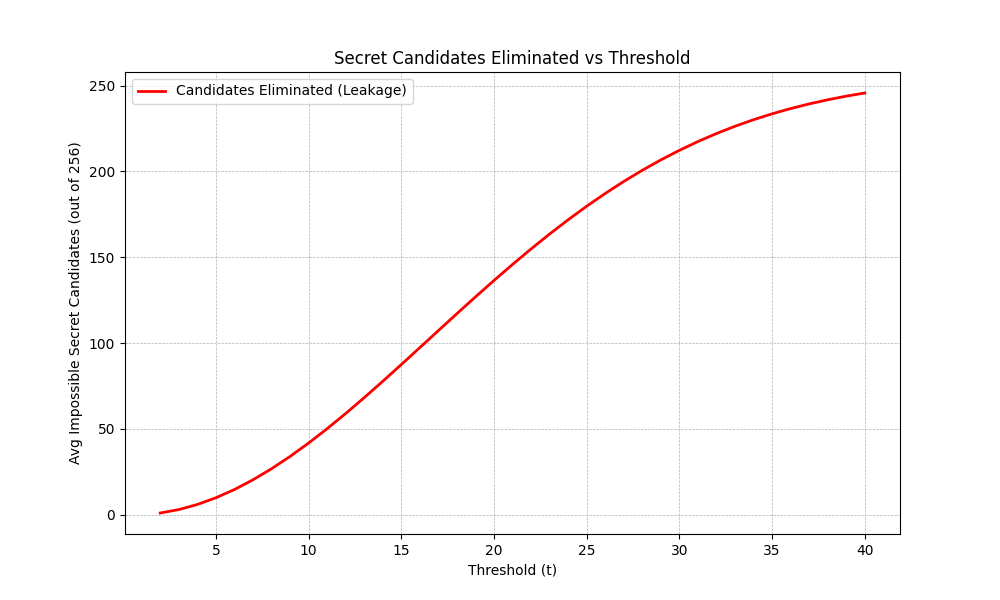
Statistical Impact
The probability that a random polynomial violates this constraint increases significantly as the threshold $t$ increases (Birthday Problem).
For a small threshold (e.g., 3), the leakage is small. However, as $t$ approaches the field size limits (e.g., $t=20$ or higher), the probability that a valid random polynomial would have colliding coefficients increases, meaning the "rejection filter" runs more often, skewing the distribution more heavily.

Here is a Python simulation that proves the reduction in search space

And here is a chart that shows how security degrades as the threshold increases:

Recommendation
Remove the check while (q.includes(w)). The coefficients should be allowed to collide with the secret and with each other to ensure uniform distribution over the finite field. The Python implementation is correct and does not include this check.